Système invariant
Un dispositif invariant par décalage temporel est un dispositif dont la sortie ne dépend pas explicitement du temps.
Un dispositif invariant par décalage temporel est un dispositif dont la sortie ne dépend pas explicitement du temps.
Définition
Si le signal d'entrée 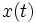 produit une sortie
produit une sortie 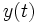 , tandis quelque soit l'entrée décalée temporellement
, tandis quelque soit l'entrée décalée temporellement 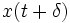 , la sortie est elle aussi décalée
, la sortie est elle aussi décalée 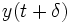 .
.
Cette propriété peut être satisfaite (mais pas obligatoirement) si la fonction de transfert du dispositif n'est pas une fonction du temps, si ce n'est dans l'expression de l'entrée et de la sortie.
Définition équivalente : Si le dispositif est invariant, alors le bloc du dispositif est commutatif avec un bloc délai arbitraire.
Pour savoir comment déterminer si un dispositif est invariant, considérons les deux dispositifs :
- Dispositif A :
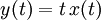
- Dispositif B :
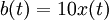
Comme le dispositif A dépend explicitement du temps t en dehors de 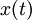 et
et 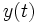 , alors le dispositif n'est pas invariant. Le dispositif B, lui, ne dépend pas explicitement du temps t et est par conséquent invariant.
, alors le dispositif n'est pas invariant. Le dispositif B, lui, ne dépend pas explicitement du temps t et est par conséquent invariant.
Exemple formel
Une preuve plus formelle de l'invariance (ou non) des dispositifs A et B ci dessus est présentée ici. Pour effectuer cette preuve, la seconde définition va être utilisée.
Dispositif A :
- A partir de l'entrée avec un décalage
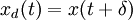
- Maintenant retardons la sortie par δ
- Clairement
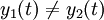 , c'est pourquoi le dispositif n'est pas invariant.
, c'est pourquoi le dispositif n'est pas invariant.
Dispositif B :
- A partir de l'entrée avec un décalage
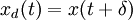
- Maintenant retardons la sortie par
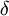
- Clairement
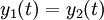 , c'est pourquoi le dispositif est invariant
, c'est pourquoi le dispositif est invariant
Exemple abstrait
Notons l'opérateur retard par 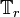 où r est la quantité par laquelle le paramètre vectoriel doit être retardé. A titre d'exemple, le dispositif "avance de 1" :
où r est la quantité par laquelle le paramètre vectoriel doit être retardé. A titre d'exemple, le dispositif "avance de 1" :
peut être représenté par la notation abstraite :
où 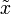 est la fonction donnée par
est la fonction donnée par
le dispositif produisant la sortie décalée
Donc 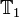 est un opérateur qui avance l'entrée vectorielle de 1.
est un opérateur qui avance l'entrée vectorielle de 1.
Supposons que nous représentions le dispositif par un opérateur 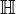 . Ce dispositif est invariant s'il commute avec l'opérateur retard, c'est-à-dire :
. Ce dispositif est invariant s'il commute avec l'opérateur retard, c'est-à-dire :
Si l'équation du dispositif est donnée par :
Alors c'est un dispositif invariant si on peut appliquer l'opérateur 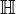 sur
sur 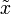 suivi de l'opérateur retard
suivi de l'opérateur retard 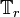 , ou appliquer l'opérateur retard
, ou appliquer l'opérateur retard 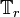 suivi de l'opérateur du dispositif
suivi de l'opérateur du dispositif 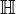 , les 2 calculs produisant un résultat équivalent.
, les 2 calculs produisant un résultat équivalent.
Appliquons l'opérateur du dispositif en premier :
Appliquer l'opérateur retard en premier donne :
Si le dispositif est invariant, alors
Voir aussi
Recherche sur Google Images : |
|
"Alors c'est un système invariant si ..." L'image ci-contre est extraite du site fr.wikipedia.org Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (67 x 18 - 1 ko - png)Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 14/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

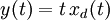
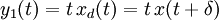
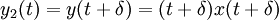
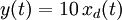
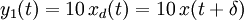
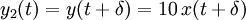
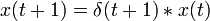
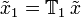
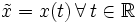
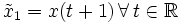
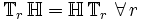
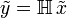
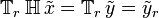
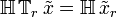
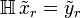

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité