Découplage
L'objectif du découplage est de transformer les fonctions de transfert ou les représentations d'états multivariables pour pouvoir commander chaque sortie indépendamment des autres.
Recherche sur Google Images :

Source image : bomatin.20six.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- En référence à la figure 7, les cœfficients R et T sont des fonctions des ... Le découplage est acceptable lorsque le module du cœfficient de transfert T... (source : freepatentsonline)
L'objectif du découplage est de transformer les fonctions de transfert ou les représentations d'états multivariables pour pouvoir commander chaque sortie indépendamment des autres.
Soit le dispositif : 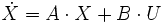 et
et 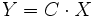 avec dim x = m; dim u = p; dim y = p
avec dim x = m; dim u = p; dim y = p
d'où : 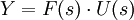 avec F (s) = C (sI − A) − 1B
avec F (s) = C (sI − A) − 1B
F est nommé matrice de transfert carré.
Approche Fonction de transfert :
En boucle fermé : Y (s) = [I. p + F (s). C (s) ] − 1F (s) C (s) Yd (s) avec Yd la consigne
Le découplage consiste à diagonaliser le fonction de transfert en boucle fermé (FTBF).
FTBF = [I. p + F (s). C (s) ] − 1F (s) C (s)
Donc le correcteur C (s) doit vérifier : [Ip + F (s) C (s) ] − 1F (s) C (s) = Ω (s) avec Ω (s) = matrice diagonale de λ1 (s)... λn (s)
On a donc : C (s) = F (s) − 1Ω (s) [I − Ω (s) ] − 1
Approche représentation d'état :
Soit le dispositif : 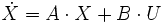 et
et 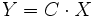
on a 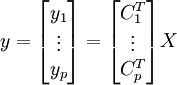
Pour y1 : 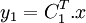
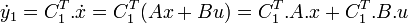
Si 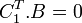 alors
alors 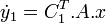
d'ou : 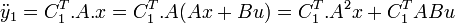
Si 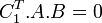 alors
alors 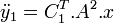
...
soit j le plus petit entier tel que 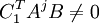
alors 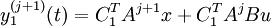
De meme pour les autres sorties : 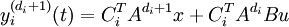
On obtient 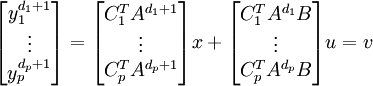
Y = Fx + Lu = v
on trouve par conséquent u = L − 1[v − Fx]
Le dispositif est découplale ssi L est inversible.
Le dispositif découplé est par conséquent transformé en sous-dispositifs : 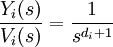 On aboutit à des intégrateurs.
On aboutit à des intégrateurs.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 14/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.


 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité