Réponse impulsionnelle
La réponse impulsionnelle d'un dispositif est la sortie du dispositif quand l'entrée est une impulsion. En effet, quand on injecte cette impulsion à un dispositif de transmission linéaire, la sortie n'est pas une impulsion mais un signal de durée finie.
Recherche sur Google Images :

Source image : f2ea.free.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Définitions :
- Mesure de la réponse entrée/sortie d'un dispositif, dans le domaine temporel, à un signal transitoire particulièrement bref en entrée.... (source : enceintehifi)
La réponse impulsionnelle d'un dispositif est la sortie du dispositif quand l'entrée est une impulsion. En effet, quand on injecte cette impulsion à un dispositif de transmission linéaire, la sortie n'est pas une impulsion mais un signal de durée finie.
Définition mathématique
Mathématiquement, cette impulsion est modélisée par une impulsion de Dirac. La réponse impulsionnelle est alors la sortie du dispositif en réponse à cette impulsion.
Soit T la représentation mathématique d'un dispositif discret (et non le dispositif lui même), c'est-à-dire qu'avec une entrée {x[n]} il produit une sortie {y[n]} suivant la relation :
T est par conséquent un opérateur qui travaille sur une suite et produit une autre suite.
Supposons qui plus est que T soit linéaire et invariant par translation temporelle. Alors toute sortie de ce dispositif peut être calculée à partir de l'entrée et de la réponse impulsionnelle qui caractérise entièrement le dispositif à partir de la relation :
Dans le cas continu, cette expression devient :
Preuve (Cas discret)
Dans un premier temps, appelons {h[k]} la sortie correspondant à l'entrée impulsion {δ[k]}
Remarquons ensuite qu'une entrée {x[k]} est une suite d'impulsion discrète décalées dans le temps. Comme le dispositif est invariant, le décalage des impulsions produit simplement une sortie elle aussi décalée (voir dispositif invariant). De plus, la linéarité du dispositif permet d'obtenir la sortie {y[n]} en calculant séparement la réponse à chacune de ses impulsions puis en les additionnant.
Calculons désormais la contribution à l'instant n de l'impulsion décalée de k0 : pour une entrée ![\left\{ x[k_0] \delta [k-k_0] \right\}](illustrations/abd03374509c853c8f5a63b642373109.png) , la sortie vaut à l'instant n,
, la sortie vaut à l'instant n, ![x[k_0] h[n-k_0]\](illustrations/e0758ec21335c9443ba60ac76fbe854e.png) .
.
La réponse totale s'obtient en sommant les contributions de l'ensemble des impulsions décalées :
On remarque qu'il s'agit d'un produit de convolution. Or il est commutatif. Nous avons par conséquent finalement :
La suite ![h\left[ n\right]](illustrations/2780fe15d3bbae2c1981125e9d0f4b1e.png) est la réponse impulsionnelle du dispositif représenté par T. Comme vous pouvez le constater, h[n] est la sortie du dispositif lorsque l'entrée est une impulsion de Dirac discrète. Des résultats identiques existent pour les dispositifs continus.
est la réponse impulsionnelle du dispositif représenté par T. Comme vous pouvez le constater, h[n] est la sortie du dispositif lorsque l'entrée est une impulsion de Dirac discrète. Des résultats identiques existent pour les dispositifs continus.
Relation avec la fonction de transfert d'un SLI
La transformée de Laplace (respectivement la transformée en Z) de la réponse impulsionnelle 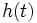 (respectivement
(respectivement ![h\left[ n\right]](illustrations/2780fe15d3bbae2c1981125e9d0f4b1e.png) ) d'un dispositif linéaire invariant (SLI) continu (respectivement discret) est identique à la fonction de transfert
) d'un dispositif linéaire invariant (SLI) continu (respectivement discret) est identique à la fonction de transfert 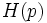 (respectivement
(respectivement 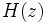 ) de ce dispositif.
) de ce dispositif.
Pour démontrer cela, il suffit d'appliquer les transformées à la relation ![y\left[ n\right] =\sum_{k}x\left[ n-k\right] h\left[ k\right]](illustrations/7778ba47fc100854eaa95f68a90622bf.png) en se souvenant qu'un produit de convolution devient un produit dans le domaine fréquentiel.
en se souvenant qu'un produit de convolution devient un produit dans le domaine fréquentiel.
Voir aussi
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 14/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

![\{y\left[ n\right]\} =T\left[ \{x\left[ n\right]\} \right]](illustrations/c2d5cb38f54391f9942c081cc0df3641.png)
![y\left[ n\right] =\sum_{k}h\left[ n-k\right] x\left[ k\right] =\sum_{k}h\left[ k\right] x\left[ n-k\right]](illustrations/3ff09bcf3cfe26426beaa1093a7de1e8.png)
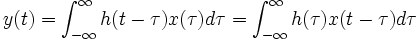
![y\left[ n\right] =\sum_{k}x\left[ k\right] h\left[ n-k\right]](illustrations/1223d4acb8052f583fac3324d7524cec.png)

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité