Commande LQG
En automatique, la Commande linéaire quadratique gaussienne dite commande LQG est une méthode qui sert à calculer le gain d'une commande par retour d'état dans un soucis spécifique de diminuer les bruits blancs.
Recherche sur Google Images :
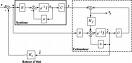
Source image : personnel.supaero.fr Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- 4.1 Principe général de la commande LQG.... deux matrices de pondération avec, comme auparavant, . \begin{displaymath} Q=Qˆ{T}\geq 0\... par l'équation classique du filtre de KALMAN à condition que le triplet \left (A, M Wˆ{1/2}, C\... (source : personnel.supaero)
- On se propose tout d'abord de mettre en place une commande LQG.... On a par conséquent à résoudre les deux équations de Riccati suivantes :... (source : laas)
- Optimal control ; Multivariable control ; Polynomial equation ; Matrix equation... Commande optimale ; Commande multivariable ; Equation polynomiale... (source : cat.inist)
En automatique, la Commande linéaire quadratique gaussienne dite commande LQG est une méthode qui sert à calculer le gain d'une commande par retour d'état dans un soucis spécifique de diminuer les bruits blancs.
La commande LQG réunit un controleur LQ (Linear Quadratic) et un estimateur de Kalman pouvant être calculé indépendemment suivant le principe de séparation. La commande LQ garantie une certaine robustesse de la boucle fermée, ce qui n'esr pas le cas de la boucle LQG.
Caractère optimal
Si on considère le dispositif suivant :
Où z est le vecteur de variables contrôlées; u est le vecteur de commande; v est un bruit blanc gaussien sur l'état et w un bruit blanc gaussien sur la sortie.
Le critère optimisé standard est de type temporel et permet d'opérer un compromis entre le temps de convergence et la consommation de commande : 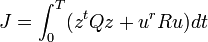 Où : z est le vecteur de variables contrôlées; u est le vecteur de commande; Q et R sont des matrices de pondérations définies positives
Où : z est le vecteur de variables contrôlées; u est le vecteur de commande; Q et R sont des matrices de pondérations définies positives
Le controleur LQG est la solution des équations :
La matrice 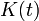 est nommée gain de Kalman du filtre de Kalman associée à la première équation. Ce filtre estime l'état du dispositif
est nommée gain de Kalman du filtre de Kalman associée à la première équation. Ce filtre estime l'état du dispositif 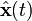 . Le gain de Kalman
. Le gain de Kalman 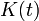 est calculé à partir des matrices
est calculé à partir des matrices 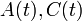 est les deux matrices de covariances
est les deux matrices de covariances 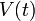 ,
, 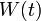 des bruits blancs gaussiens
des bruits blancs gaussiens 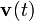 et
et 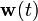 et de l'état d'origine
et de l'état d'origine 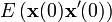 . Le gain de Kalman est calculé par résolution de l'équation de d matrix Riccati,
. Le gain de Kalman est calculé par résolution de l'équation de d matrix Riccati,
Soit 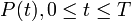 le gain de Kalman est ,
le gain de Kalman est ,
La matrice 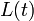 est le gain du correcteur LQ. Cette matrice est déterminée par es matrices
est le gain du correcteur LQ. Cette matrice est déterminée par es matrices 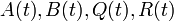 et
et 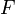 par résolution de l'équation de Riccati,
par résolution de l'équation de Riccati,
Soit 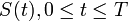 il vient,
il vient,
On peut observer la similarité entre les deux équations différentielles : la première est dans le sens de la flèche du temps alors que la seconde est à rebours. Cela vient de la dualité entre les problèmes de contrôle et d'estimation.
Lorsque 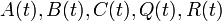 et les matrices de covariances
et les matrices de covariances 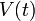 ,
, 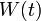 ne dépendent pas du temps, le controleur LQG est invariant dans le temps et les équations deviennent des équations de Riccati (équation de Riccati) algébriques.
ne dépendent pas du temps, le controleur LQG est invariant dans le temps et les équations deviennent des équations de Riccati (équation de Riccati) algébriques.
La commande LQG est optimale au sens de la norme H2. Pour faire le lien avec les techniques fréquentielles de type H∞ : il est envisageable de réaliser un optimisation dans le domaine fréquentiel au sens de la norme H2 sur le même schéma de synthèse d'une commande H∞. La synthèse H2 peut être réalisée sur les mêmes entrées-sorties que la synthèse Hinifni, tout juste sera-t-il indispensable de régler les pondérations fréquentielles.
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 14/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

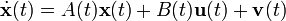
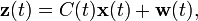
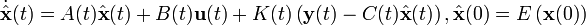
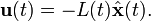
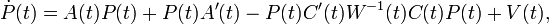
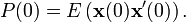
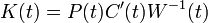
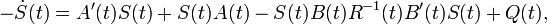
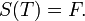
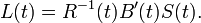

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité